[클러스터링] K-MEANS(K-평균 군집)

1. K-MEANS란?

대표적인 분리형 군집화 알고리즘 가운데 하나이며, 각 군집은 하나의 중심(centroid)을 가지고 있다. 각 개체는 가장 가까운 중심에 할당되며, 같은 중심에 할당된 개체들이 모여 하나의 군집을 형성한다. 사용자가 사전에 군집 수(k)가 정해야 알고리즘을 실행할 수 있다.

 

2. 원리

• K-means는 EM 알고리즘을 기반으로 작동합니다. EM알고리즘은 크게 Expectation 스텝과 Maximization 스텝으로 나뉘어져 있다.
• 군집 수 k를 2로 결정. 최초 군집의 중심(빨간색 점)을 랜덤 초기화합니다

• 모든 개체들(파란색 점)을 가장 가까운 중심에 군집(녹색 박스)으로 할당하며, 이것이 Expectation 스텝이다.

• 중심을 군집 경계에 맞게 이동하며, 이것이 Maximization 스텝이다.

• 모든 개체들을 가장 가까운 중심에 군집(보라색 박스)으로 할당한다.(즉 Expectation 스텝 적용)

• Maximization 스텝을 또 적용해 중심 이동. Expectation과 Maximization 스텝을 반복 적용해도 결과가 바뀌지 않거나(=해가 수렴), 사용자가 정한 반복수를 채우게 되면 학습이 끝나게 된다.

3. 소스코드

Github : https://github.com/Byeongin-Jeong/clustering.git

# 라이브러리 import
import time
import os
import matplotlib.pyplot as plt
import pandas as pd
import plotly.graph_objs as go
import numpy as np
import csv
import random

from pandas import merge
from scipy import stats
from collections import Counter
from plotly.offline import init_notebook_mode, iplot
from sklearn.cluster import KMeans
from sklearn.utils import shuffle
from sklearn.decomposition import PCA

init_notebook_mode(connected=True)

# 2D 그래프로 표현
def gettrace(patient_clusters, cluster_num):
    r = random.randrange(1,255)
    g = random.randrange(1,255)
    b = random.randrange(1,255)
    return go.Scatter(x = patient_clusters[patient_clusters.cluster == cluster_num]['x'],
                   y = patient_clusters[patient_clusters.cluster == cluster_num]['y'],
                   name = "Cluster {}".format(cluster_num+1),
                   mode = "markers",
                   marker = dict(size = 10,
                                 color = "rgba({0}, {1}, {2}, 0.5)".format(r, g, b),
                                 line = dict(width = 1, color = "rgb(0,0,0)")))

# 최적의 클러스터 개수를 추출하기 위한 함수
def elbow(X):
    sse = []
    for i in range(1, 10):
        km = KMeans(n_clusters=i, init='k-means++', random_state=0)
        km.fit(X)
        sse.append(km.inertia_)
        print (km.inertia_)
    plt.plot(range(1, 10), sse, marker='o')
    plt.xlabel('cluster count')
    plt.ylabel('SSE')
    plt.show()

src_dic = {}
dst_dic = {}

loopcnt = 0

f = open('data/netflow_dump.csv', 'r', encoding='utf-8')
rdr = csv.reader(f)

for line in rdr:
    src = line[0]
    dst = line[1]

    src_dic.setdefault(src, set())
    src_dic[src].add(dst)
f.close()

dst_li = [len(x) for x in src_dic.values()]

# 고유한 DST ADDR 수집
id_dst_dic = {}
for dst_set_li in src_dic.values():
    for x in dst_set_li:
        if x not in id_dst_dic:
            id_dst_dic.setdefault(x, len(id_dst_dic))

print("# of left dst:%d" % (len(id_dst_dic)))

id_src_dic = {}

# DST ADDR 개수
all_dst_count = len(id_dst_dic)

produc_columns = [x for x in id_dst_dic.values()]
produc_columns.sort()
produc_columns.insert(0, 'srcip')

df = pd.DataFrame(columns=produc_columns)

for srcip, dsts in src_dic.items():
    src_dst_vec = [0] * all_dst_count

    id_src_dic[len(id_src_dic)] = srcip

    for dstip in dsts:
        src_dst_vec[id_dst_dic[dstip]] = 1

    # 첫번째 columns를 src ip로한 dataframe 생성
    src_dst_vec.insert(0, srcip)
    df.loc[len(id_src_dic)] = [n for n in src_dst_vec]

# 데이터를 랜덤으로 섞는다    
df = shuffle(df)

# 데이터의 70%만 추출
tran_lenght = int(len(df) * 0.7)

# 학습 데이터와 테스트 데이터로 분리
train_data = df[df.columns[1:]][:tran_lenght+1]
test_data = df[df.columns[1:]][tran_lenght:]

print ("70% data count: ", tran_lenght)

# 최적의 클러스터 확인
elbow(train_data)

cols = df.columns[1:]

clusternum = 4

# 데이터 학습
kmeans = KMeans(n_clusters = clusternum)
kmeans.fit(train_data)

# 테스트 데이터 클러스터
test_clusters = df[:][tran_lenght:]
test_clusters["cluster"] = kmeans.predict(test_data)
test_clusters.tail()

# 좌표 데이터 추출
pca = PCA(n_components = 2)
test_clusters['x'] = pca.fit_transform(test_clusters[cols])[:, 0]
test_clusters['y'] = pca.fit_transform(test_clusters[cols])[:, 1]
test_clusters.tail()

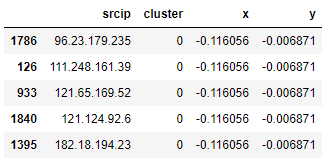
# dataframe 재정의(ip, cluster, x, y)
patient_clusters = test_clusters[['srcip', 'cluster', 'x', 'y']]
patient_clusters.tail()

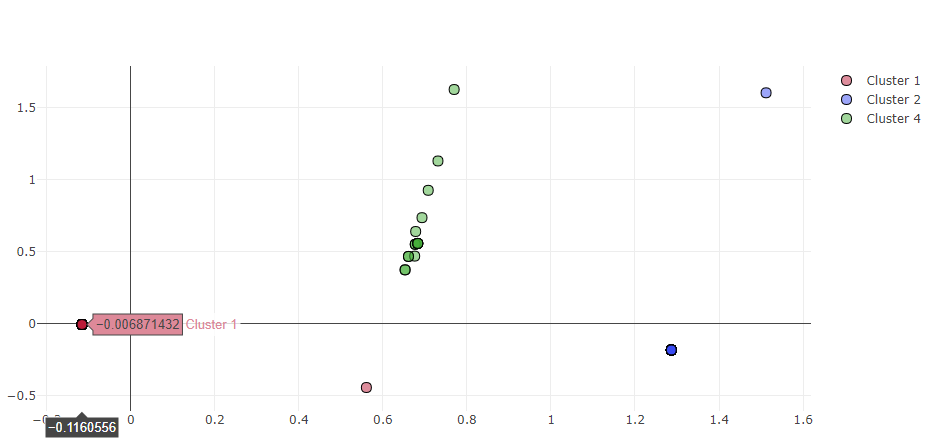
# 2D 그래프로 시각화
data = []
for idx in range(clusternum):
    data.append(gettrace(patient_clusters, idx))

iplot(data)

 

4. 분석

• load한 데이터를 Dataframe으로 정의

• 학습 데이터

• 테스트 데이터

• 최적의 클러스터 개수를 찾기 위한 elow 함수의 결과
  그래프가 급격히 하락하다가 데이터 변화가 크게 없는 구간인 3~4 구간이 최적의 클러스터 개수이다

• train 데이터로 학습 후 test 데이터로 추출한 클러스터 결과

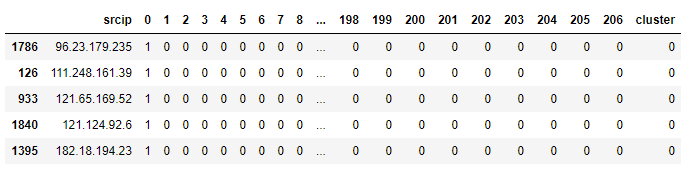
• 시각화하기 위한 x, y좌표 데이터 생성

• srcip, cluster, x, y 데이터 재정의

• 2D 그래프 시각화

• K-Means 모델의 경우 클러스터링 개수를 지정해줘야 하는 단점과 모든 데이터가 클러스터링이 되기 때문에, 이상감지에 대한 명확한 정의가 없을 경우 이상 데이터 추출이 어렵다.

5. 결론

K-Means의 경우 모든 데이터를 군집화 하기 때문에 빠르고 사용자가 원하는 클러스터링 개수에 적절한 군집 성능을 보여주지만, 최초 센터점이 랜덤이기 때문에 예상하지 못한 결과가 도출될 수 있다. 정상 데이터 이외에 발생하는 이상 데이터를 사용자에게 알리는게 목적이므로, 모든 데이터가 군집이 되며 클러스터링 개수가 정의 필요한 K-means는 이상감지에 적합하지 않다고 판단된다.